The overall design and operation of declared-strategy voting systems was introduced in the previous chapter. We explained that DSV systems are designed to allow voters to express their preferences in terms of a strategy that results in a vote that is both expressive and effective. Throughout the chapter the existence of such voting strategies was assumed, but no attention was paid to their form or how they might be determined. In this chapter voting strategies will be explored in detail and a method for rational strategy formulation will be presented.
Because rational strategy formulation is a complicated process, it is
crucial that an automated strategy formulation system be provided so
that voters need not study decision theory in order to cast a vote.
Here we develop a DSV strategy formulator that can process
information supplied by a voter and produce a rationally-optimal
strategy. Figure 
illustrates how the strategy
formulator fits into the model developed in Chapter 3.
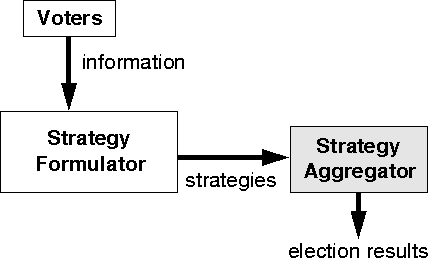
Figure: Declared-strategy voting with strategy formulator
Before formalizing the notion of voting strategies, we examine the types of strategies voters might use (consciously or subconsciously) in a traditional election with three or more alternatives.
Some voters may adopt a sincere strategy, refusing to vote for any alternative besides their favorite, regardless of the favorite's chances of winning.
Other voters may exhibit more strategic behavior, taking into account both their own preferences and the likely preferences of other voters. For example, these voters may adopt a don't waste my vote strategy in which they vote for their sincerely preferred alternative only if that alternative is likely to be one of the top contenders. A variation on this is the vote against last choice strategy in which voters vote for whichever alternative has the best chance of beating their least favorite alternative.
Some voters may be fairly indifferent between the alternatives and may select strategies based on factors not related to their preferences for the various alternatives:
All of the above strategies may be considered rational (assuming they are consistent with a voter's preferences) in that they further the outcome most desired by the voter. Throughout this text we assume that voters are rational if they take the actions they believe are most likely to lead to their most preferred outcome -- regardless of whether it is reasonable for them to prefer that outcome. Thus, in order to behave rationally, a voter must have a set of preferences, a set of beliefs, and a strategy consistent with his or her preferences and beliefs.
While it is reasonable that voters should seek to vote rationally -- and thus possibly insincerely -- it has not heretofore been possible for the voter to express a rational voting strategy in a traditional election. DSV provides the vehicle for expressing a rational strategy; however, the mathematics associated with formulating the optimal rational strategy can be formidable, certainly beyond the capability of a mathematically unsophisticated, albeit politically astute voter.
In this chapter we develop an automated strategy formulator that
produces strategies which optimally represent the rational voter in a
DSV election. Section introduces a formal method for
determining a voter's rationally optimal strategy.
Section discusses methods for determining and quantifying
beliefs about the preferences of other voters and introduces a novel
method that scales better than those found in the literature.
Section examines the specification of strategies for voters
who are indifferent between the alternatives. These elements are tied
together and a decision-theoretic strategy formulator is presented in
Section .