In this chapter we have seen how the expected-utility model can be
used to produce optimal strategies based on a voter's preferences and
predictions about the outcome of an election. A voter's preferences
may be represented as utility values on a finite scale, say from 0 to
10. In addition, voters who are indifferent between alternatives must
also supply tie-breaking rules. Depending on the pivot-probability
method used, we might also ask voters to supply a measure of their
attitude towards risk. Given this information, a computer can
calculate the optimal decision-theoretic strategy for each voter and
submit it to the strategy aggregator, as shown in
Figure 
. Thus, voters need not understand the process
of formulating an expected-utility maximization function to use this
system.
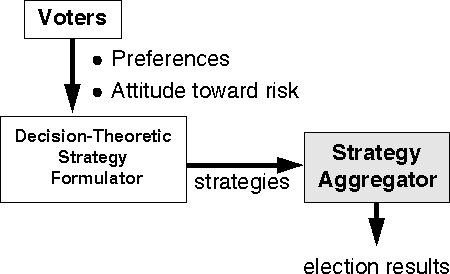
Figure: A model of declared-strategy voting with
decision-theoretic strategy formulator
A strategy formulator that uses our 2-D Gaussian method for
calculating pivot probabilities formulates an optimal strategy for an
N-alternative plurality-rule election as shown in
Figure .
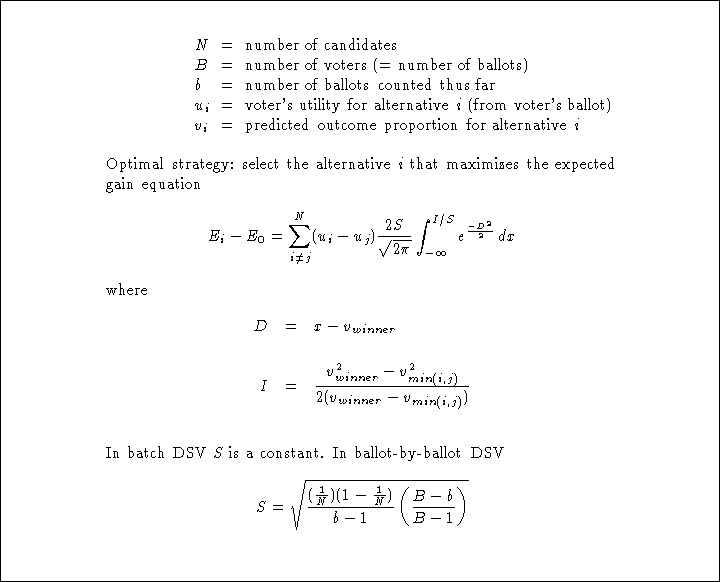
Figure: Summary of formulas for optimal plurality-rule strategy with 2-D
Gaussian pivot probabilities
Note that we ask voters to submit their sincere utility values for all candidates. Our system calculates the optimal decision-theoretic strategy based on these values, enabling voters to vote strategically while simultaneously revealing their sincere preferences. Thus it is generally advantageous for voters to submit their sincere utility values. However, as we discuss later, occasionally voters who have the necessary knowledge to formulate sophisticated strategies might not find it to their advantage to reveal their sincere utility values (and will act accordingly).