If there were a way to elicit sincere preference information from all voters prior to an election, this information could be made public and all voters would have the opportunity to use it in formulating their strategies. In the absence of sincere preference information, information about the strategies the other voters plan to use (sincere or otherwise) is still useful. However once the information is published, voters will adjust their strategies to take into account the preferences of others. Myerson and Weber [74] describe a series of polls in which voters are given the results after each poll. Eventually, they predict, a voting equilibrium may arise in which ``the perceptions arising from the publication of the poll lead the voters to behave in a manner that in turn justifies the predictions of the poll.'' They then go on to prove that at least one voting equilibrium must exist in all elections. In this scenario, all voters have equal access to the information that they need to vote strategically. However, conducting an election in this manner is unattractive because it would require voters to go repeatedly to the polls. This sort of election is likely to take a long time and have low voter turnout.
One way to side-step the problem of supplying voters with equal access to information is to allow them to cast votes that are contingent on the votes of others. While some parliamentary voting rules allow absent voters to cast proxies that are contingent on the votes of others (for example, the system used by the French National Assembly [44]), contingency voting is not a feature of most voting schemes. Contingency voting has a fundamental problem in that non-contingent votes must be counted before contingent votes; if all voters wish to cast contingent votes there is no way to count any votes without introducing an element of chance to decide which votes to count first. Another problem with contingency voting is the difficulty in evaluating complex contingency rules, especially when the number of voters is large or when votes are tallied at many geographically distributed precincts. But contingency voting is nonetheless appealing because it allows voters without voter preference information to vote strategically. In addition, examination of contingency votes may provide insight into the true preferences of the electorate that is not otherwise available when voters vote insincerely.
The advent of high-speed computers and computer networks makes it feasible to tally contingency ballots in a reasonable amount of time. In addition, computers can handle complicated vote aggregation methods, making possible voting procedures not previously considered. With that in mind, we now sketch the design of an information-neutral voting system that employs contingency voting. We call this system a declared-strategy system because voters declare the computations used to determine their vote. The computation represents the voter's strategy in formulating a vote, rather than simply the outcome of that decision process. Following game-theoretic practice, we assume that each voter decides on a strategy prior to the election that includes a specification of how the vote will be cast given any contingency. A declared strategy is a first-order function of the ``state'' of the election. For example, in the 1992 US Presidential election, a Perot supporter who preferred Clinton to Bush might have used the strategy: vote for Perot if he has received more votes than Clinton so far, otherwise vote for Clinton.
In our system, voters submit their strategies to the election computer. The computer evaluates the voters' strategies using the current election tally and other state information. The strategies are then aggregated to determine the election outcome. Thus, our basic system requires a strategy aggregator module that includes a strategy evaluator for evaluating each strategy and a vote accumulator for tallying the results. However, there are many ways in which we might proceed to flesh out the details of our DSV strategy aggregator. We developed two types of approaches, which could be considered as the extreme ends of a spectrum of approaches: batch aggregation and ballot-by-ballot aggregation. Both of these techniques may be combined with any positional aggregation technique (plurality, approval, Borda, etc.). We describe these two approaches below.
The ballot-by-ballot technique involves making an outcome prediction,
evaluating one selected ballot based on that prediction, updating the
prediction, and repeating until all ballots have been evaluated. The
initial prediction may be set to zero or based on some initialization
procedure. As the ballots are evaluated, they are added to a running
tally. The first ballot selected will be evaluated with no
information (unless the system is initialized with some information)
while the last ballot selected will be evaluated with perfect
information. The strategy aggregator needed to conduct an election
using this technique can be represented by the machine model shown in
Figure 
. This technique results in outcomes that
may be dependent on the order in which the ballots are selected for
evaluation. As a result, the election results may not be stable.
Note that the traditional voting systems discussed in
Chapter always produce the same outcome given the
same set of ballots (with the exception of some PR implementations
that employ randomness), and thus are completely stable. Gibbard's
mixed decision scheme [54] is an example of a highly
unstable voting system, as the outcome is based almost entirely on
chance. DSV systems may be designed to minimize instability (or even
eliminate it at the expense of increased manipulability).
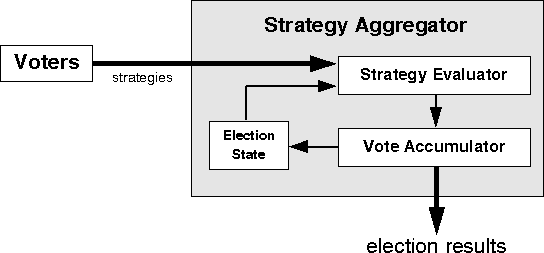
Figure: A machine model of ballot-by-ballot declared-strategy voting
Any ordering might be selected for ballot evaluation; however, a random ordering is perhaps the most fair, while considerably reducing the opportunities for the system to be manipulated. Although the results may be unstable, there are voting situations in which this ramification is acceptable. For example, John M. Brimacombe, managing director for a small British software company, found an unstable voting system to be the best solution to a voting problem faced by his employees four years ago. Brimacombe explained that, due to limited resources, he decided to reduce the recreational USENET newsgroups that were offered on his company's server from approximately 300 groups to about 100 groups. He concocted a cumulative voting scheme in which each employee could distribute 100 votes over his or her favorite newsgroups. Each group was then given a weight based on its average traffic volume and the groups were ranked according to their vote totals divided by their weights. He then went down the list, selecting the top ranked newsgroups in order until the sum of the average traffic of the selected groups equaled the limit that he had set for the company. When he announced the results to his five employees, all were dissatisfied. Some groups had received many surplus votes at the expense of others that just barely missed the cutoff. The employees asked to repeat the voting procedure with their newly acquired knowledge about the preferences of their colleagues. However, the second vote proved to be not much better than the first, and the voting was repeated several more times. It is likely that had the voting continued indefinitely, an equilibrium would have developed eventually. But in the interest of time, Brimacombe decided to choose an alternate voting system. This time he selected one employee at random and had him announce his votes. He then selected another employee to vote after observing the votes of the first employee. This procedure continued until everyone had cast their votes. All employees were satisfied with the outcome, despite the fact that it was likely to have been slightly different had the employees voted in a different order [59].
The procedure Brimacombe ended up using is similar to ballot-by-ballot DSV. However, Brimacombe's method would not scale well if more voters were to be polled because it requires voting to take place serially. Ballot-by-ballot DSV improves on this procedure by allowing each voter to submit a strategy prior to the election that represents the voter no matter when it is selected for evaluation. Thus voters need not wait to see how their peers voted before casting their ballots.
The batch technique involves making an outcome prediction based on the sincere outcome point, evaluating all ballots based on this prediction, updating the prediction based on the previous evaluations, and repeating until an equilibrium is reached. This technique simulates the situation described by Myerson and Weber [74] in which voters are repeatedly polled until the results of a poll justify the predictions of the previous poll. However, batch DSV requires that the voters be polled only once.
The batch technique may be preferable to the ballot-by-ballot
technique in some situations because it need not introduce chance into
the declared-strategy system. Although at least one equilibrium
always exists [74], batch DSV may not reach an equilibrium
under all circumstances and therefore requires the use of an arbitrary
termination condition. A machine model of batch DSV is shown in
Figure .
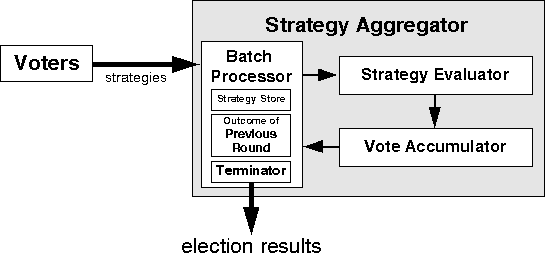
Figure: A machine model of batch declared-strategy voting
The idea of using multiple batched rounds to provide decision-makers with increasing amounts of information has been applied in a variety of applications, most notably the simultaneous ascending auction protocol used by the Federal Communications Commission (FCC) for recent electromagnetic spectrum auctions. This auction method was proposed by economists Paul Milgrom, Robert Wilson, and Preston McAfee. It allows multiple licenses to be bid on simultaneously in a multi-round process. The results of each round are announced prior to the start of the next round, thus providing bidders with increasing information about their competitors' strategies as the auction progresses. Bidding proceeds until an equilibrium is reached or a sufficient number of rounds have transpired that the auction is terminated. The FCC conducted their auctions in three stages, each with different conditions on the minimum activity of each bidder. This forced bidders to participate and reveal information in every round rather than waiting to observe their competitors' strategies before bidding. The auction was conducted online to facilitate the lengthy bidding process. The use of the simultaneous ascending procedure resulted in companies being able to win groups of complementary spectrum allocations (which is often difficult when auctions occur serially) and in the U.S. government receiving payments much higher than expected [68].
Batch DSV operates in a similar manner to the simultaneous ascending auction. However, formulating an optimal voting strategy is a somewhat simpler problem than formulating an optimal bidding strategy, especially when the election involves independent alternatives. DSV thus allows voters to submit a strategy that will represent them throughout the election rather than resubmitting their ballots after each round. In the next chapter we present an automated, rational strategy formulator that formulates optimal voting strategies on behalf of voters.