The evaluation criteria introduced in Chapter 
are
useful for exploring the properties of declared-strategy voting from a
theoretical standpoint. These criteria as applied to DSV with
plurality rule are summarized in Figure . When DSV is
used in conjunction with other voting rules it may have slightly
different properties.
DSV systems inherit some properties from the positional voting procedures they employ. Because none of the single-stage positional systems are guaranteed to select a Condorcet winner, DSV systems do not satisfy the Condorcet criterion. However, as with some positional systems, some DSV systems may guarantee that the Condorcet loser is never selected.
Brams and Fishburn have analyzed the ability of plurality and approval voting to select a Condorcet winner when voters use poll data to vote strategically [17]. They concluded: ``Under plurality voting, the Condorcet candidate will always lose if he is not one of the top two candidates identified by the poll'' and ``the Condorcet candidate will always win if he is one of the top two candidates identified by the poll.'' They also concluded: ``Under approval voting, a non-Condorcet candidate may be helped, and the Condorcet candidate hurt, by a poll, whether or not the Condorcet candidate is one of the top two candidates identified by the poll'' and ``adjustments caused by continual polling may (i) have no effect on the outcome, (ii) reinforce or undermine a particular outcome, or (iii) induce cycling.'' This analysis is applicable to DSV systems that employ plurality or approval voting as these systems essentially simulate what happens when voters use poll data to vote strategically. While it is certainly a deficiency of plurality DSV that the Condorcet candidate cannot win unless it is one of the top two in the polls, it is a deficiency shared with plurality voting in many real election situations. A similar problem occurs also in the STV system when the Condorcet candidate is the candidate with the fewest first-place votes.
DSV systems have several properties in common with single transferable vote (STV) systems. When DSV is used in conjunction with plurality rule (with each voter casting a single vote, regardless of the number of alternatives) it is indeed quite similar to STV. Both systems allow voters to cast a ballot with ordered choices that is evaluated into a single vote. In fact, STV is essentially a simple DSV system (absent preference intensities) in which second-choice voting occurs only when there is complete certainty that a voter's first choice has enough votes to win or near certainty that a voter's first choice cannot win. As with STV, DSV is Pareto-optimal and neutral, but not necessarily consistent or monotonic. The difficulty of exploiting these violations in either system make the lack of consistency and monotonicity insignificant for most practical purposes.
DSV violates the independence from irrelevant alternatives criterion for the same reason that STV violates it: the outcome may be affected by the removal or addition of alternatives. However, this violation becomes more serious in DSV systems that involve randomness. When randomness is involved, the same profile of ordinal preferences will not necessarily result in the same election outcome every time the votes are counted. The Cambridge implementation of STV suffers from the same problem, but is of little practical concern because the effects of randomness have proved to be quite minor and result in little instability [47]. But the instability associated with some types of DSV may render them unacceptable for some purposes.
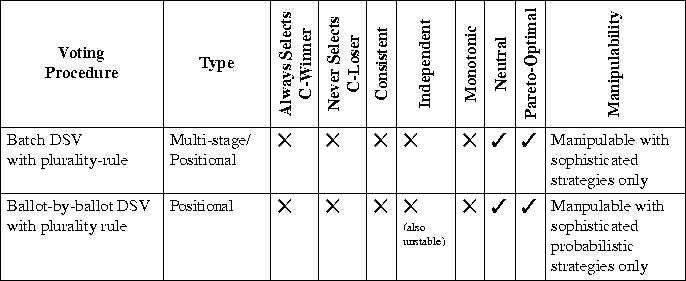
Figure: Properties of declared-strategy voting
As with STV, DSV results in elections with high average effectiveness because it allows voters to be effective even when their first choice is not likely to win. This in turn discourages manipulation because manipulation is not necessary to cast an effective vote. Furthermore, the complexity of both systems make opportunities for manipulation difficult (although not impossible) to identify when there is a large number of voters.
When the number of voters is small, opportunities for manipulation may become apparent to knowledgeable voters using batch DSV. For example, suppose 21 voters hold the following ordinal preferences for three alternatives.
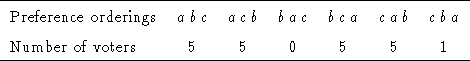
Thus if all voted sincerely in a plurality election, a would win with 10 votes and b would finish last with 5 votes. Assuming the appropriate cardinal preferences (not shown for the sake of simplicity) batch plurality rule DSV would result in the supporters of b all voting for c, their second choice. Thus the results of the DSV election would be as follows:
Now suppose that voters with preference ordering abc are able to obtain the cardinal preference information for all the other voters. If these voters have sufficient knowledge they will figure out that if three of them adopt a sophisticated strategy, misrepresenting their preferences as bac, they can change the outcome of the election. With three voters misrepresenting their preferences, the ordinal preferences appear to be:
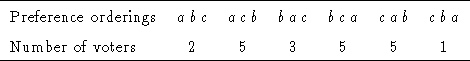
With this preference ordering, the batch plurality DSV results are:
Thus, manipulation has changed the outcome of the election. In this case other voters may adopt counter strategies that will prevent this manipulation from being successful, assuming they posses sufficient knowledge and information. But the only way manipulation can be rendered impossible is if sufficient amounts of randomness are built into the DSV system. In ballot-by-ballot DSV, manipulation is only possible by using sophisticated probabilistic strategies that take into account the probability that the ballots will be calculated in a particular order.
From the knowledge-needed-to-manipulate perspective, DSV without randomness is still more difficult to manipulate than the positional voting systems because knowledge of voters' ordinal preferences is not always sufficient; knowledge of voters' complete cardinal preferences may be required.
The concept of expressiveness, introduced in
Chapter , is rarely discussed in evaluations of
voting systems. This may be due to the fact that voting systems are
generally thought of only as a means to make a decision; thus, they
are evaluated only in terms of their ability to make a good decision.
But once a decision has been made it is often important that people
understand why the decision was made. Especially when the decision is
the selection of a representative or elected official, it is equally
important to understand how much of a mandate the winner really had.
It is also important for the satisfaction of the electorate that
voters feel that their vote meant something, even if their preferred
candidate did not win.
When there are a small group of voters assembled for a meeting, discussions prior to a vote help people to understand the degree to which each alternative is supported and why. Furthermore, a dynamic process often occurs in which those who realize there is little support for their preferred alternative eventually abandon that alternative and argue for their second choice. Lakeman provides a graphic example of this behavior:
Rowland Hill ...records that, when he was teaching in his father's school, his pupils were asked to elect a committee by standing beside the boy they liked best. This first produced a number of unequal groups, but soon the boys in the largest groups came to the conclusion that not all of them were actually necessary for the election of their favourite and some moved on to help another candidate, while on the other hand the few supporters of an unpopular boy gave him up as hopeless and transferred themselves to the candidate they considered the next best. The final result was that a number of candidates equal to the number required for the committee were each surrounded by the same number of supporters, with only two or three boys left over who were dissatisfied with all those elected. This is an admirable example of the use of the STV [63].
Indeed, STV has been praised for simulating the human behavior that occurs in situations where voter preferences are well known. However, STV falls short in its ability to simulate this behavior completely because it does not take into account the intensity of preferences. It is likely that the school boys who favored one boy only slightly more than another were the first to abandon their favorites, while those who strongly favored one boy held out the longest or refused to support a second choice regardless of the electability of their first choice. DSV is unique among the voting systems presented in its ability to model this behavior.
DSV is more expressive than any of the positional voting systems because it allows voters to express the intensity of their preferences and because it allows voters to cast votes that are simultaneously effective and expressive. Although voting systems involving utilities are often criticized because they are based on the arguable assumption that interpersonal comparisons of cardinal measures are meaningful, they do offer voters a better chance at expressing themselves then do positional voting systems. DSV combines the best of both worlds, allowing voters to express themselves with cardinal preferences while employing an aggregation system that does not rely on interpersonal comparisons of these preferences: a voter's cardinal preferences are used only to determine an optimal voting strategy for that individual, but they are not aggregated into the election tally. However, cardinal preference data is available for analysis after the election. This data may be useful, for example, to distinguish between a winner generally preferred only slightly to the runner-up, and a winner greatly preferred to the runner-up. This distinction, which cannot be made with ordinal preference data alone, may be useful for guiding future policy decisions.
DSV is also superior in its ability to allow voters to express
preferences extraneous to their utilities for the candidates, but
still relevant to the election. Using DSV, voters who are indifferent
between the candidates may select underdog, bandwagon, abstention, or
random strategies, or other strategies reflective of their
preferences. For example, as suggested in Chapter ,
voters who are indifferent between the candidates running in their
party's primary, may have a desire to help make their party appear
unified. Thus they would choose a bandwagon strategy. Other
indifferent voters might enjoy personal satisfaction from knowing they
voted or might be interested in contributing to a high rate of voter
participation in their precinct. By choosing a random strategy or an
abstention strategy these voters can add to the total number of votes
cast without influencing the outcome and without registering a
preference. Voters who are indifferent between individual
alternatives but have an opinion about the alternatives as a
group -- for example, all are excellent, or none are
acceptable -- can also express themselves with DSV.