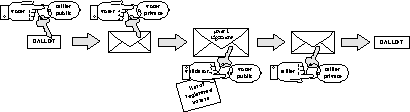
Figure 2: A Simplistic Voting Protocol
Chaum proposed the first published cryptographic voting protocol in a 1981 paper on anonymous electronic mail and digital pseudonyms [3]. This protocol uses public key cryptography and relies on rosters of digital pseudonyms to conceal the identity of voters. However, the protocol does not guarantee that the identity of voters cannot be traced. Chaum later proposed a protocol which unconditionally conceals the identity of voters [5]. However, elections conducted with this protocol can be disrupted by a single voter. Although Chaum's protocol can detect such disruptions, it cannot recover from them without restarting the entire election [11].
In 1985 Cohen (a.k.a. Benaloh) and Fischer published a description of a secure election scheme in which it is very difficult for dishonest voters to disrupt the election [7]. However, the scheme does not protect the privacy of individuals from the election authority. Cohen later presented extensions to this scheme which distribute the power of government and offer more privacy protection [6]. Benaloh claims this scheme is ``reasonably practical'' and cites political problems as a greater hindrance to implementation than technical problems. However, he also acknowledges that knowledge of college-level mathematics is required for voters to independently verify election results [2]. In addition, because of the scheme's large communication complexity, casting a vote may take an unacceptably long time [17].
In 1994 Benaloh and Tuinstra proposed a set of verifiable secret-ballot election protocols that do not allow voters to prove the contents of their votes [1]. Unlike the other cryptographic protocols discussed here, these protocols require voters to vote inside a voting booth. The authors maintain that the simplest of their protocols does not require computations on the part of the voter that are outside ``the range of normal human ability.'' However, the more complex protocols that have fewer requirements for trusting election authorities would require the voter to bring a personal computing device into the voting booth. Even the Full Scale Receipt-Free Protocol does not guarantee that voters cannot be coerced, unless one or more election authorities are trustworthy. Although not a practical solution for Internet voting, the receipt-free nature of this system is significant because it prevents voters from participating in vote buying schemes.
A number of other cryptographic voting schemes have been proposed that require interactions between voters. These schemes, including [9], may be useful in a board room setting, but are not suitable for most large-scale elections.
The more practical cryptographic schemes do not require any interaction between voters or use of specialized equipment. However, none of these schemes prevent vote buying. One of the more simplistic of these schemes requires two election authorities: a validator and a tallier. In this scheme, shown in Figure 2, voters encrypt their ballots with the tallier's public key, sign them, and forward them to the validator. The validator strips off the voters' signatures, checks to make sure the ballots were submitted by registered voters who had not yet voted, and forwards the ballots to the tallier. The tallier decrypts the ballots and records the votes. This scheme prevents non-registered voters from voting and registered voters from voting multiple times. However, it only protects voters' privacy if the tallier and validator do not collude. In addition, it does not provide a mechanism for voters to use to verify that their votes were counted correctly.

Figure 2: A Simplistic Voting Protocol
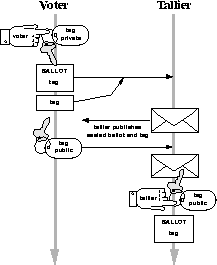
Figure 3: Phase 2 of the Two Agency Protocol
In the Two Agency Protocol developed by Nurmi, Salomaa, and
Santean [15], the responsibilities of validating registered
voters and computing and publishing the results of the election are
divided between two agencies, as in the simplistic scheme. In the
first phase of this protocol, the validator sends a large prime
identification tag to each of n voters who have previously reported
an intention to vote. The validator then sends the tallier a list of
all n identification tags (with no record of the corresponding
voters). In the second phase, each voter B sends the tallier the pair
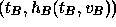 , where
, where 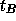 is the voter's tag,
is the voter's tag,
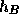 is a cryptographic hash function of two variables, and
is a cryptographic hash function of two variables, and 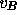 is the vote. The tallier then publishes
is the vote. The tallier then publishes 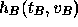 . B
responds by sending the tallier the pair
. B
responds by sending the tallier the pair 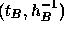 ,
allowing the tallier to determine
,
allowing the tallier to determine 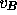 . When the voting period is
over, the tallier publishes a list of each
. When the voting period is
over, the tallier publishes a list of each 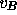 and its
corresponding
and its
corresponding 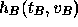 . At this point each voter can
confirm that his or her vote was counted properly. In phase 3, any
voter who discovers that his or her vote was lost or not counted
properly can protest by submitting the triple
. At this point each voter can
confirm that his or her vote was counted properly. In phase 3, any
voter who discovers that his or her vote was lost or not counted
properly can protest by submitting the triple 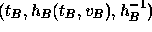 . Because
. Because 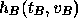 was published in
phase 2, the tallier cannot deny the error. In phase 4 (optional),
voters can change their votes by repeating the procedures in phases 2
and 3 with a different hash function. (Note, the hash functions used
in this protocol can be implemented as public/private key pairs, as
shown in Figure 3.) One of the biggest problems
with this protocol is that if the validator and tallier collude they
can determine the mapping between B and
was published in
phase 2, the tallier cannot deny the error. In phase 4 (optional),
voters can change their votes by repeating the procedures in phases 2
and 3 with a different hash function. (Note, the hash functions used
in this protocol can be implemented as public/private key pairs, as
shown in Figure 3.) One of the biggest problems
with this protocol is that if the validator and tallier collude they
can determine the mapping between B and 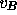 [18].
[18].
The One Agency Protocol is identical to the Two Agency Protocol,
except for the tag distribution procedure in phase 1. In the One
Agency Protocol, tags are distributed by the tallier (there is no
validator) using an ANDOS (all-or-nothing disclosure of secrets)
protocol for secret selling of secrets. This solves the collusion
problem, but not the vote buying problem. In addition, it requires
the use of a very complex protocol for distributing tags. Another
problem with both the One and Two Agency Protocols is that the tallier
may cast votes for all voters who have been assigned a 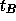 but do
not exercise their right to vote [18,15]. The One
Agency Protocol is more private than the Two Agency Protocol, but is
also considerably more difficult to implement.
but do
not exercise their right to vote [18,15]. The One
Agency Protocol is more private than the Two Agency Protocol, but is
also considerably more difficult to implement.
When Chaum first introduced the concept of blind signatures in 1982, he suggested that blind signatures could be used for secret ballot elections. Ten years later, Fujioka, Okamoto, and Ohta developed a practical voting scheme that uses blind signatures to solve the collusion problem inherent in protocols like the Two Agency Protocol without significantly increasing the overall complexity of the protocol [10]. (A number of other, less satisfactory blind signature protocols have also been proposed. Sako, for example, proposed a protocol that is simpler but does not completely prevent election administrators from linking ballots with the voters who cast them [16].) The Sensus protocol is based closely on the Fujioka, Okamoto, and Ohta scheme. The main difference between these schemes emerges after the voter has submitted the encrypted ballot to the tallier. In the Sensus protocol, the tallier responds by sending a receipt to the voter. The voter may submit the decryption key immediately after receiving this receipt, completing the entire voting process in one session (verification must still wait until the election is over). In the Fujioka, Okamoto, and Ohta protocol the tallier responds by placing the encrypted ballot on a list that is published after all voters vote. Thus, a voter cannot submit his or her decryption key until after the voting phase of the election is over. As a result, votes cannot be cast in a single session.
The Sensus protocol satisfies most of the core properties well; however, it fails to correct one of the problems inherent in the One and Two Agency protocols: the election administrators (in this case the validator) can cast votes for abstaining voters. These invalid votes can be detected by the abstaining voters themselves or by an auditor who checks the signatures on all the validation requests submitted. However, there is no way to identify the invalid ballots and remove them from the tally. If voters who wish to abstain submit blank ballots, then this problem can be avoided.
Another problem with the Sensus protocol is that it requires the voter to participate in a complex set of transactions in order to cast a vote. However, by including a pollster module in the Sensus system, we allow the voter to perform these transactions with ease.