Having sketched the framework for a declared-strategy voting system, we will now describe three ways of assembling the components, each of which results in a system with different properties. The main difference between these systems lies in the way we account for uncertainty. We will explain each system and show the outcome each would produce given an example set of voter preference information.
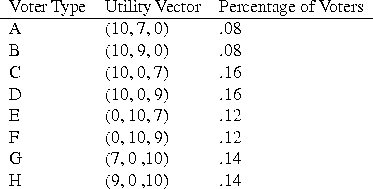
In our example election, we will assume for simplicity that no voters are indifferent between any pair of candidates; thus we need not consider tie-breaking rules. The utility vectors for our voters are as follows:

Our first system relies on random methods for calculation uncertainty. In this system voters submit their preference information and tie-breaking strategies without knowing the uncertainty factor that will be used. Just prior to the evaluation phase, a random uncertainty factor is calculated. The ballots are then evaluated using the batch technique and the random uncertainty value. This procedure results in a system that elicits sincere preference information from most voters. The only voters for whom it is not necessarily rationally optimal to submit sincere preference information are those who have found a probabilistic sophisticated strategy (this would require prior knowledge of the preferences of the other voters). Because such a strategy is not likely to be found by many voters, this system is highly resistant to manipulation. However, it is also unstable, as the results may vary depending on the random uncertainty value chosen.
For example, with a random uncertainty factor of .027, the evaluation would proceed as follows:
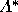 equation for each voter using equal pivot probabilities.
This will result in a predicted outcome point which assumes that all
voters will vote sincerely. In this case that point occurs at (.48,
.24, .28).
equation for each voter using equal pivot probabilities.
This will result in a predicted outcome point which assumes that all
voters will vote sincerely. In this case that point occurs at (.48,
.24, .28).
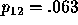 ,
, 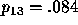 , and
, and 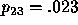 .
.
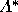 equation for each voter using the new pivot
probabilities and calculate a new predicted outcome point. In this
example, the F and H voters will select insincere strategies while
all the other voters will select sincere strategies. The new
predicted outcome point will occur at (.62, .12, .26).
equation for each voter using the new pivot
probabilities and calculate a new predicted outcome point. In this
example, the F and H voters will select insincere strategies while
all the other voters will select sincere strategies. The new
predicted outcome point will occur at (.62, .12, .26).
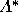 equations for each voter again, this time
using the second-round pivot probabilities. In this round, the E
voters join the F and H voters in selecting insincere strategies.
The second-round predicted outcome point is (.62, 0, .38).
equations for each voter again, this time
using the second-round pivot probabilities. In this round, the E
voters join the F and H voters in selecting insincere strategies.
The second-round predicted outcome point is (.62, 0, .38).
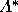 equations for each voter again, this time
using the third-round pivot probabilities. In this round the H
voters return to their sincere strategies, resulting in a
third-round predicted outcome point of (.48, 0, .52).
equations for each voter again, this time
using the third-round pivot probabilities. In this round the H
voters return to their sincere strategies, resulting in a
third-round predicted outcome point of (.48, 0, .52).
Depending on the random uncertainty factor selected in this example,
equilibrium outcomes may occur at (.48, 0, .52), (.72, .24, 0), or
(.62, .24, .14). Voters wishing to use a sophisticated strategy may
do so by selecting insincere utilities which will result in a possible
outcome set more favorable to their preferred candidates. But unless
they can find a sophisticated strategy that will produce the same
outcome regardless of the uncertainty factor used, the sophisticated
strategy will not always result in the desired outcome. For example,
if all voters submit sincere strategies here, candidate 1 will win
whenever 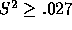 . A and B voters might select a
sophisticated strategy in which they would submit the utility
vector (9, 10, 0). This would result in a victory for 1 if
. A and B voters might select a
sophisticated strategy in which they would submit the utility
vector (9, 10, 0). This would result in a victory for 1 if 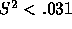 . Thus, depending on the range of possible random values, voters
may be able to increase their chances of achieving a preferred outcome
by voting insincerely, but they can rarely guarantee a preferred
outcome this way. In addition, by voting insincerely, voters lose
their opportunity to make their true preferences known.
. Thus, depending on the range of possible random values, voters
may be able to increase their chances of achieving a preferred outcome
by voting insincerely, but they can rarely guarantee a preferred
outcome this way. In addition, by voting insincerely, voters lose
their opportunity to make their true preferences known.
Our second system is similar to the first; however, it involves repeating the evaluation process many times, using different uncertainty values for each repetition. The uncertainty values would be selected so as to find all possible outcomes for the set of voter preferences submitted. This system is also highly resistant to manipulation. However, it suffers from being indecisive; this system selects a set of outcomes rather than a single outcome.
Returning to our example, if all voters submit sincere utility vectors, the outcome set will contain the possible outcomes listed above: (.48, 0, .52), (.72, .24, 0), and (.62, .24, .14). This outcome set selects either candidate 1 or candidate 3 as the winner. Voters who submit insincere utility vectors may be able to shift the outcome points or increase or decrease the number of points in the outcome set. In this case, if A and B voters submitted the utility vector (9, 10, 0), the outcome space would contain the points: (.60, .40, 0) (.32, .40, .28). This outcome set selects either candidate 1 or candidate 2 as the winner. Thus supporters of candidate 1 are still not able to remove outcome points which select other candidates from the outcome set. Depending on what procedures are used to further narrow the outcome set, they may have advantaged or disadvantaged candidate 1 by voting insincerely.
Our final system uses a known arbitrary uncertainty value (or alternately an uncertainty value based on voter preferences --- this would be computable by anyone who is able to obtain voter preference information prior to the election). This system is both stable and decisive. The only voters for whom it is not necessarily rationally optimal to submit sincere preference information are those who have found a sophisticated strategy. Thus the system resists manipulation (although not as well as the other two systems).
Once again, our example shows that each of three possible outcomes is
possible depending on the uncertainty value used. Because voters know
the uncertainty value in advance, they may formulate sophisticated
strategies in which 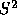 is a constant. (Even if we select
is a constant. (Even if we select 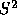 based on some aggregation of voter preference information, voters with
prior information about the presences of others could deduce this
number in advance. Likewise if voters submitted individual risk
factors to be used for
based on some aggregation of voter preference information, voters with
prior information about the presences of others could deduce this
number in advance. Likewise if voters submitted individual risk
factors to be used for 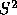 , some voters may be able to obtain this
information in advance; however, such an approach is likely to further
complicate the process of formulating a sophisticated strategy and
thus reduce the number of voters who do so successfully.) So, if
, some voters may be able to obtain this
information in advance; however, such an approach is likely to further
complicate the process of formulating a sophisticated strategy and
thus reduce the number of voters who do so successfully.) So, if
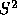 was selected to be .01, candidate 3 would win if all voters
vote sincerely. A and B voters might be tempted to use a
sophisticated strategy and submit the insincere utility vector (9, 10,
0). This would result in a victory for candidate 1. However,
anticipating that A and B voters will use a sophisticated strategy, E
and F voters would also use a sophisticated strategy and submit the
insincere utility vector (0, 9, 10). This would result in a victory
for candidate 3. In this example, voters cannot change the winner by
using a sophisticated strategy (assuming all voters who could benefit
from using a sophisticated strategy act accordingly); however, this is
not always the case.
was selected to be .01, candidate 3 would win if all voters
vote sincerely. A and B voters might be tempted to use a
sophisticated strategy and submit the insincere utility vector (9, 10,
0). This would result in a victory for candidate 1. However,
anticipating that A and B voters will use a sophisticated strategy, E
and F voters would also use a sophisticated strategy and submit the
insincere utility vector (0, 9, 10). This would result in a victory
for candidate 3. In this example, voters cannot change the winner by
using a sophisticated strategy (assuming all voters who could benefit
from using a sophisticated strategy act accordingly); however, this is
not always the case.