


Next: Pivot Probability Calculations
Up: A Framework for
Previous: A Framework for
Before determining what strategies should be permitted and how they
should be formulated, we considered the strategies that rational
voters might like to use. We assume that voters are rational if they
take the actions they believe are most likely to lead to their most
preferred outcome. We are not concerned with whether it is rational
for them to prefer that outcome. As already discussed, several
authors have suggested that voters may use expected-utility models
involving their personal preferences and the probable preferences of
the rest of the electorate to determine their rationally optimal
strategies. In fact, Black [3] used the approach outlined
by McKelvey and Ordeshook [15] to model the 1968 and 1972
Canadian Federal elections and found ``significant empirical support
for the role of probabilities in the multicandidate calculus of
voting.''
McKelvey and Ordeshook [15] deduced that in N-candidate
elections one can setup N difference equations that calculate the
expected gain in utility associated with a given voter voting for a
particular candidate rather than abstaining. Assuming that the voter
has established a set of utility values 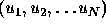 specifying his or her personal utility for candidate N winning the
election, and assuming that the probability of a three-way tie is
negligible, the difference equations for a plurality election which
selects a single winner can be written in the form:
specifying his or her personal utility for candidate N winning the
election, and assuming that the probability of a three-way tie is
negligible, the difference equations for a plurality election which
selects a single winner can be written in the form:
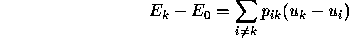
where 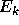 is the expected utility associated with voting for
candidate k,
is the expected utility associated with voting for
candidate k, 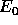 is the expected utility associated with
abstaining, and
is the expected utility associated with
abstaining, and 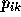 (which we shall refer to as a pivot
probability) is the probability that the voter will be
decisive in creating or breaking a tie between i and k. Note
that the voter affects the election result if and only if he or she
casts a vote that creates or breaks a first-place tie. A rational
voter will vote for the candidate k that maximizes the
(which we shall refer to as a pivot
probability) is the probability that the voter will be
decisive in creating or breaking a tie between i and k. Note
that the voter affects the election result if and only if he or she
casts a vote that creates or breaks a first-place tie. A rational
voter will vote for the candidate k that maximizes the 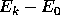 equations.
equations.
Consider, for example, a three candidate plurality election. The
voter can combine the difference equations for his or her two most
preferred candidates (denoted 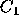 and
and 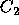 ) to form the
equation:
) to form the
equation:
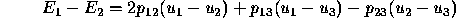
Thus 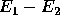 can be used to determine the candidate for which it
is rationally optimal to vote:
can be used to determine the candidate for which it
is rationally optimal to vote:

The McKelvey and Ordeshook model is ambiguous about how the voter
should vote if 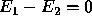 . When this occurs, the voter cannot
expect to be better off voting for
. When this occurs, the voter cannot
expect to be better off voting for 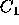 rather than
rather than 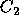 or vice
versa. For example, this situation occurs when the voter is indifferent
between all candidates. In this case the voter might decide to
abstain, make a random selection, adopt a bandwagon strategy (voting
for the candidate most likely to win), or adopt an underdog strategy
(voting for the candidate most likely to lose). Although unlikely,
this situation can also occur when the voter is not indifferent
between all candidates. In this case the voter may choose any of the
above options or vote for
or vice
versa. For example, this situation occurs when the voter is indifferent
between all candidates. In this case the voter might decide to
abstain, make a random selection, adopt a bandwagon strategy (voting
for the candidate most likely to win), or adopt an underdog strategy
(voting for the candidate most likely to lose). Although unlikely,
this situation can also occur when the voter is not indifferent
between all candidates. In this case the voter may choose any of the
above options or vote for 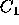 as a show of support.
as a show of support.
Hoffman [13] paraphrased the 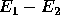 equation into a
critical value formula:
equation into a
critical value formula:
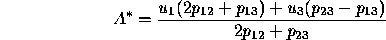
indicating that a voter should vote for 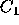 if
if 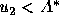 and
and
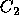 if
if 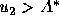 . We shall use Hoffman's formulation
throughout the remainder of this paper.
. We shall use Hoffman's formulation
throughout the remainder of this paper.
In developing our declared-strategy voting system, we assume that
rational voters will develop declared strategies consistent with the
expected-utility model. Therefore, to accommodate these voters, our
system need only accept strategies based on the expected-utility
equations for the voting procedure being used (simple plurality,
approval, etc.) and the number of candidates under consideration. In
fact, a tie-breaking rule (for example, bandwagon strategy) plus a
single strategy function in terms of utilities and pivot probability
estimates should be sufficient for representing the declared strategy
of any rational voter. This approach even accommodates those voters
who wish to vote despite being indifferent between all candidates.
These voters may submit equal utility values for all candidates and
have their votes based solely on their tie-breaking rules. One
situation where this might prove useful involves voters who are
indifferent between the candidates running in their party's primary
but want to vote for whichever candidate is most likely to win in
order boost the winner's share of the vote and make their party appear
more unified.
The expected-utility calculus can also be extended for elections that
use decision rules other than plurality and that select more than one
winner. For example, Merrill [16] presented a model in
which a voter's utility differences for a pair of candidates was
multiplied by the difference in votes that the voter awarded to each
member of that pair of candidates. This accommodates a voting system
such as Borda count in which the voter casts N-1 votes for his or
her most preferred candidate, N-2 votes for his or her second most
preferred candidate, and so on.
For the purposes of this paper,
all voters in a given election are essentially
using the same (rational)
voting strategy with differing parameters; thus, voters need only submit the
relevant parameters as part of their ballots.
In this system we will ask
voters to submit their utility values for each candidate on a scale
of 0 to 10, as well as their tie-breaking rules.
Depending on the probability
calculation method used, we may also require the voters to submit a
number that indicates their attitude toward risk.
The other parameters---the probability values---can be calculated
on a voter's behalf
as explained in the next section.
Thus, voters need
not understand the process of formulating an expected-utility
maximization function to use this system.
Note that we ask voters to submit their sincere utility values for all
candidates. Our system will calculate the optimal decision-theoretic
strategy based on these values, enabling voters to vote strategically
while simultaneously revealing their sincere preferences. Thus it is
generally advantageous for voters to submit their sincere utility
values. However, as we will discuss later, voters who have the
necessary knowledge to formulate sophisticated strategies might not
find it to their advantage to reveal their sincere utility values (and
will act accordingly).



Next: Pivot Probability Calculations
Up: A Framework for
Previous: A Framework for
Lorrie Faith Cranor
Thu Apr 25 14:31:14 CDT 1996
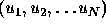 specifying his or her personal utility for candidate N winning the
election, and assuming that the probability of a three-way tie is
negligible, the difference equations for a plurality election which
selects a single winner can be written in the form:
specifying his or her personal utility for candidate N winning the
election, and assuming that the probability of a three-way tie is
negligible, the difference equations for a plurality election which
selects a single winner can be written in the form:
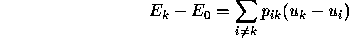
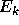 is the expected utility associated with voting for
candidate k,
is the expected utility associated with voting for
candidate k, 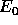 is the expected utility associated with
abstaining, and
is the expected utility associated with
abstaining, and 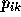 (which we shall refer to as a pivot
probability) is the probability that the voter will be
decisive in creating or breaking a tie between i and k. Note
that the voter affects the election result if and only if he or she
casts a vote that creates or breaks a first-place tie. A rational
voter will vote for the candidate k that maximizes the
(which we shall refer to as a pivot
probability) is the probability that the voter will be
decisive in creating or breaking a tie between i and k. Note
that the voter affects the election result if and only if he or she
casts a vote that creates or breaks a first-place tie. A rational
voter will vote for the candidate k that maximizes the 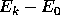 equations.
equations.
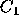 and
and 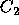 ) to form the
equation:
) to form the
equation:
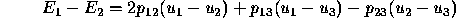
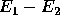 can be used to determine the candidate for which it
is rationally optimal to vote:
can be used to determine the candidate for which it
is rationally optimal to vote:

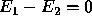 . When this occurs, the voter cannot
expect to be better off voting for
. When this occurs, the voter cannot
expect to be better off voting for 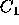 rather than
rather than 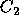 or vice
versa. For example, this situation occurs when the voter is indifferent
between all candidates. In this case the voter might decide to
abstain, make a random selection, adopt a bandwagon strategy (voting
for the candidate most likely to win), or adopt an underdog strategy
(voting for the candidate most likely to lose). Although unlikely,
this situation can also occur when the voter is not indifferent
between all candidates. In this case the voter may choose any of the
above options or vote for
or vice
versa. For example, this situation occurs when the voter is indifferent
between all candidates. In this case the voter might decide to
abstain, make a random selection, adopt a bandwagon strategy (voting
for the candidate most likely to win), or adopt an underdog strategy
(voting for the candidate most likely to lose). Although unlikely,
this situation can also occur when the voter is not indifferent
between all candidates. In this case the voter may choose any of the
above options or vote for 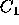 as a show of support.
as a show of support.
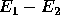 equation into a
critical value formula:
equation into a
critical value formula:
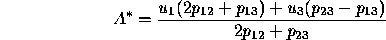
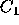 if
if 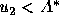 and
and
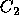 if
if 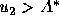 . We shall use Hoffman's formulation
throughout the remainder of this paper.
. We shall use Hoffman's formulation
throughout the remainder of this paper.